목차
# 선형 회귀(Linear Regression)
- 알려진 다른 관련 데이터 값을 사용하여 알 수 없는 데이터의 값을 예측하는 데이터 분석 기법
- 단순 선형 회귀 분석
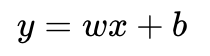
- 다중 선형 회귀 분석

- 실제값과 예측값에 대한 오차에 대한 식
- 목적 함수(Objective function) = 함수의 값을 최소화/최대화하는 목적을 가진 함수
- 비용 함수(Cost function) = 값을 최소화하려는 함수 = 손실 함수(Loss function)
=> 비용 함수는 단순히 실제값과 예측값에 대한 오차를 표현하면 되는 것이 아닌 예측값의 오차를 줄이는 일에 최적화된 식이어야 함
# 로지스틱 회귀(Logistic Regression)
- 둘 중 하나를 결정하는 문제인 이진 분류(Binary Classification)과 같은 문제를 풀기 위한 대표적인 알고리즘
- 시그모이드 함수(Sigmoid function)
- 출력이 0과 1 사이의 값을 가지면서 S자 형태로 그려지는 함수
- σ로 축약해서 표현하기도 함
- 입력된 데이터에 대해 0과 1사이의 값을 출력하여 해당 값이 둘 중 하나에 속할 확률로 해석할 수 있도록 만들어줌
- 경사 하강법을 사용하여 가중치 w를 찾아내지만 비용 함수로 평균 제곱 오차를 사용하지 않음
=> 평균 제곱 오차를 비용 함수로 사용하면 경사 하강법을 사용하였을 때 로컬 미니멈에 빠질 가능성이 높기 때문 - 가중치 w를 최소화하는 아래의 어떤 함수를 목적 함수라고 하자 => f = 비용함수
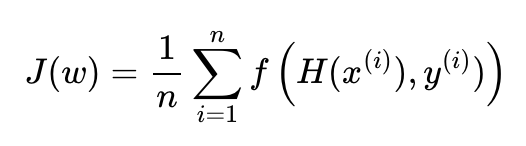
- 로지스틱 회귀에서 찾아낸 비용 함수 = 크로스 엔트로피(Cross Entropy) 함수
- 가중치를 찾기 위해서 크로스 엔트로피 함수의 평균을 취한 함수 사용
- 소프트맥스 회귀의 비용 함수이기도 함
# 소프트맥스 회귀(Softmax Regression)
- 3개 이상의 선택지 중에서 1개를 고르는 다중 클래스 분류 문제를 위한 알고리즘
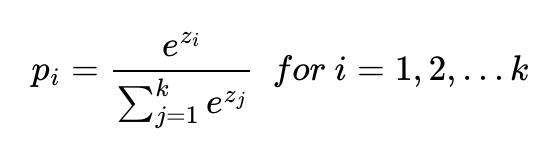

- 소프트맥스 함수
- 모델의 출력을 확률로 해석할 수 있게 변환해주는 연산
- 분류 문제를 풀 때 선형 모델과 소프트맥스 함수를 결합하여 예측
- 위의 사진에서 p1, p2, p3 = 1번 클래스가 정답일 확률, 2번 클래스가 정답일 확률, 3번 클래스가 정답일 확률
=> p1, p2, p3 각각의 값은 0과 1 사이의 값으로 총 합은 1이 됨
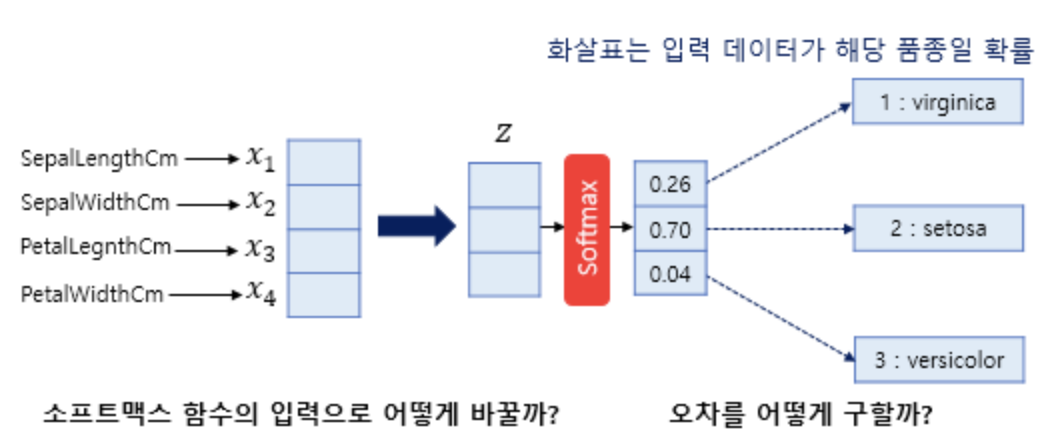
- 모델이 4차원 벡터를 입력 받아서 어떤 가중치 연산을 통해 소프트맥스 함수의 입력으로 사용되는 3차원 벡터(z)로 변환한다.

- 소프트맥스 함수의 출력은 분류하고자 하는 클래스의 개수만큼 차원을 가지는 벡터로 예측값과 비교를 할 수 있는 실제의 표현 방법이 있어야 한다.
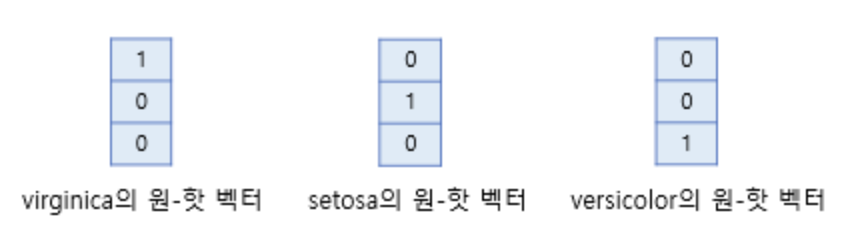
- 소프트맥스 회귀에서는 실제값을 원-핫 벡터로 표현
- 학습을 할 때는 소프트맥스가 필요하지만 추론을 할 때는 확률의 최대값을 도출하므로 원-핫 벡터를 사용한다.
# 활성 함수(activation function)
- 활성 함수를 이용해서 딥러닝에서는 선형모델로 나온 출력물을 비선형모델로 변활시킬 수 있음
=> 변형시킨 벡터 = 잠재 벡터, Hidden 벡터 - 입력값으로 벡터가 아닌 하나의 실수값을 받는다.
- 활성 함수를 쓰지 않으면 딥러닝은 선형 모형과 차이가 없음
- 시그모이드 함수나 tanh 함수는 전통적으로 많이 쓰이던 활성 함수지만 딥러닝에서는 ReLU 함수를 많이 사용함
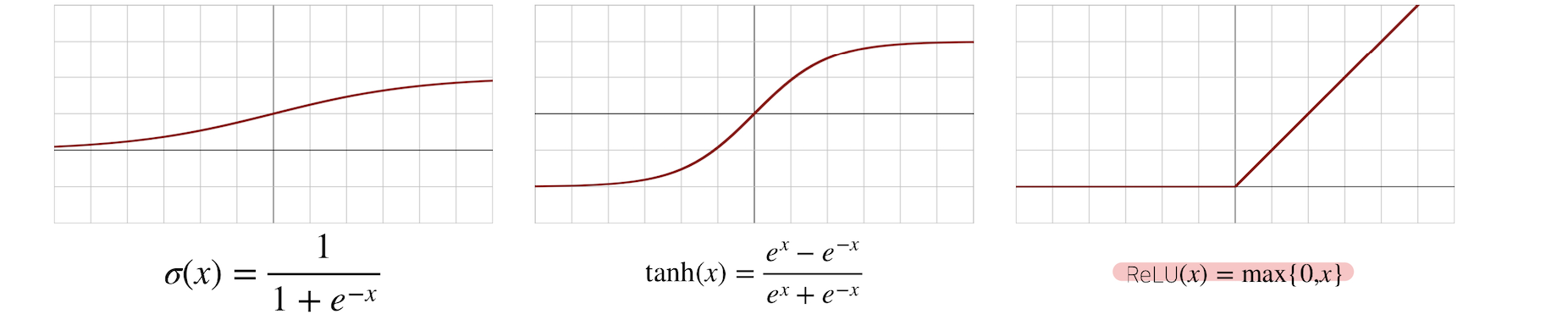
# 신경망
- 선형모델과 활성함수(activation function)를 합성한 함수
- 다층 퍼셉트론 = 신경망이 여러층 합성된 함수
- 층을 여러개 쌓는 이유
- 층이 깊을수록 목적 함수를 근사하는데 필요한 뉴런(노드)의 숫자가 훨씬 빨리 줄어들어 좀 더 효율적인 학습이 가능
- 층이 깊어질수록 적은 parameter로도 훨씬 복잡한 함수 표현 가능! But 최적화시키기 어려워짐
- 층을 여러개 쌓는 이유
# 역전파 알고리즘(back propagation)
- 순전파(forward propagation) = 입력층에서 출력층으로 향하는 순차적인 신경망 계산
- 역전파 = 출력층에서 입력층 방향으로 계산하면서 가중치를 업데이트
- 역전파 알고리즘은 합성함수 미분법인 연쇄법칙(chain-rule) 기반 자동미분(auto-differentiation)을 사용
- 각 노드의 텐서 값을 컴퓨터가 기억해야 미분 계산 가능!
# 참고자료
선형 회귀란 무엇인가요? - 선형 회귀 - AWS
Amazon SageMaker는 고품질 기계 학습 모델(ML)을 빠르게 준비, 빌드, 훈련, 배포할 수 있는 완전관리형 서비스입니다. Amazon SageMaker Autopilot은 사기 탐지, 이탈 분석, 표적 마케팅과 같은 분류 및 회귀
aws.amazon.com
07-05 역전파(BackPropagation) 이해하기
인공 신경망이 순전파 과정을 진행하여 예측값과 실제값의 오차를 계산하였을 때 어떻게 역전파 과정에서 경사 하강법을 사용하여 가중치를 업데이트하는지 직접 계산을 통해 이해해봅시다.…
wikidocs.net
'딥러닝' 카테고리의 다른 글
| [개념] Word Embedding, Word2Vec, GloVe (0) | 2023.02.09 |
|---|---|
| [개념] Bag-of-Words, Naive Bayes Classifier (0) | 2023.02.09 |
| [개념] 한국어 전처리 패키지(Text Preprocessing Tools for Korean Text) (0) | 2023.01.25 |
| [개념] 어간 추출(Stemming) 및 표제어 추출(Lemmatization) (0) | 2023.01.22 |
| [개념] 토큰화(Tokenization) (0) | 2023.01.20 |
# 선형 회귀(Linear Regression)
- 알려진 다른 관련 데이터 값을 사용하여 알 수 없는 데이터의 값을 예측하는 데이터 분석 기법
- 단순 선형 회귀 분석
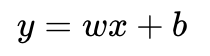
- 다중 선형 회귀 분석

- 실제값과 예측값에 대한 오차에 대한 식
- 목적 함수(Objective function) = 함수의 값을 최소화/최대화하는 목적을 가진 함수
- 비용 함수(Cost function) = 값을 최소화하려는 함수 = 손실 함수(Loss function)
=> 비용 함수는 단순히 실제값과 예측값에 대한 오차를 표현하면 되는 것이 아닌 예측값의 오차를 줄이는 일에 최적화된 식이어야 함
# 로지스틱 회귀(Logistic Regression)
- 둘 중 하나를 결정하는 문제인 이진 분류(Binary Classification)과 같은 문제를 풀기 위한 대표적인 알고리즘
- 시그모이드 함수(Sigmoid function)
- 출력이 0과 1 사이의 값을 가지면서 S자 형태로 그려지는 함수
- σ로 축약해서 표현하기도 함
- 입력된 데이터에 대해 0과 1사이의 값을 출력하여 해당 값이 둘 중 하나에 속할 확률로 해석할 수 있도록 만들어줌
- 경사 하강법을 사용하여 가중치 w를 찾아내지만 비용 함수로 평균 제곱 오차를 사용하지 않음
=> 평균 제곱 오차를 비용 함수로 사용하면 경사 하강법을 사용하였을 때 로컬 미니멈에 빠질 가능성이 높기 때문 - 가중치 w를 최소화하는 아래의 어떤 함수를 목적 함수라고 하자 => f = 비용함수
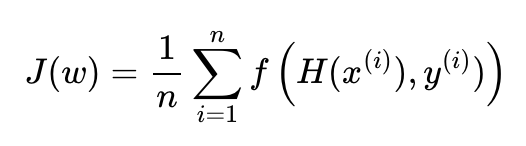
- 로지스틱 회귀에서 찾아낸 비용 함수 = 크로스 엔트로피(Cross Entropy) 함수
- 가중치를 찾기 위해서 크로스 엔트로피 함수의 평균을 취한 함수 사용
- 소프트맥스 회귀의 비용 함수이기도 함
# 소프트맥스 회귀(Softmax Regression)
- 3개 이상의 선택지 중에서 1개를 고르는 다중 클래스 분류 문제를 위한 알고리즘
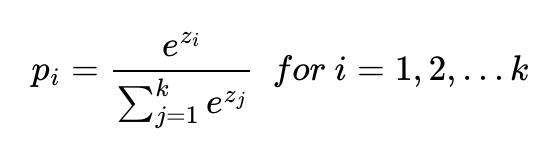

- 소프트맥스 함수
- 모델의 출력을 확률로 해석할 수 있게 변환해주는 연산
- 분류 문제를 풀 때 선형 모델과 소프트맥스 함수를 결합하여 예측
- 위의 사진에서 p1, p2, p3 = 1번 클래스가 정답일 확률, 2번 클래스가 정답일 확률, 3번 클래스가 정답일 확률
=> p1, p2, p3 각각의 값은 0과 1 사이의 값으로 총 합은 1이 됨

- 모델이 4차원 벡터를 입력 받아서 어떤 가중치 연산을 통해 소프트맥스 함수의 입력으로 사용되는 3차원 벡터(z)로 변환한다.

- 소프트맥스 함수의 출력은 분류하고자 하는 클래스의 개수만큼 차원을 가지는 벡터로 예측값과 비교를 할 수 있는 실제의 표현 방법이 있어야 한다.
- 소프트맥스 회귀에서는 실제값을 원-핫 벡터로 표현
- 학습을 할 때는 소프트맥스가 필요하지만 추론을 할 때는 확률의 최대값을 도출하므로 원-핫 벡터를 사용한다.

# 활성 함수(activation function)
- 활성 함수를 이용해서 딥러닝에서는 선형모델로 나온 출력물을 비선형모델로 변활시킬 수 있음
=> 변형시킨 벡터 = 잠재 벡터, Hidden 벡터 - 입력값으로 벡터가 아닌 하나의 실수값을 받는다.
- 활성 함수를 쓰지 않으면 딥러닝은 선형 모형과 차이가 없음
- 시그모이드 함수나 tanh 함수는 전통적으로 많이 쓰이던 활성 함수지만 딥러닝에서는 ReLU 함수를 많이 사용함

# 신경망
- 선형모델과 활성함수(activation function)를 합성한 함수
- 다층 퍼셉트론 = 신경망이 여러층 합성된 함수
- 층을 여러개 쌓는 이유
- 층이 깊을수록 목적 함수를 근사하는데 필요한 뉴런(노드)의 숫자가 훨씬 빨리 줄어들어 좀 더 효율적인 학습이 가능
- 층이 깊어질수록 적은 parameter로도 훨씬 복잡한 함수 표현 가능! But 최적화시키기 어려워짐
- 층을 여러개 쌓는 이유
# 역전파 알고리즘(back propagation)
- 순전파(forward propagation) = 입력층에서 출력층으로 향하는 순차적인 신경망 계산
- 역전파 = 출력층에서 입력층 방향으로 계산하면서 가중치를 업데이트
- 역전파 알고리즘은 합성함수 미분법인 연쇄법칙(chain-rule) 기반 자동미분(auto-differentiation)을 사용
- 각 노드의 텐서 값을 컴퓨터가 기억해야 미분 계산 가능!
# 참고자료
선형 회귀란 무엇인가요? - 선형 회귀 - AWS
Amazon SageMaker는 고품질 기계 학습 모델(ML)을 빠르게 준비, 빌드, 훈련, 배포할 수 있는 완전관리형 서비스입니다. Amazon SageMaker Autopilot은 사기 탐지, 이탈 분석, 표적 마케팅과 같은 분류 및 회귀
aws.amazon.com
07-05 역전파(BackPropagation) 이해하기
인공 신경망이 순전파 과정을 진행하여 예측값과 실제값의 오차를 계산하였을 때 어떻게 역전파 과정에서 경사 하강법을 사용하여 가중치를 업데이트하는지 직접 계산을 통해 이해해봅시다.…
wikidocs.net
'딥러닝' 카테고리의 다른 글
| [개념] Word Embedding, Word2Vec, GloVe (0) | 2023.02.09 |
|---|---|
| [개념] Bag-of-Words, Naive Bayes Classifier (0) | 2023.02.09 |
| [개념] 한국어 전처리 패키지(Text Preprocessing Tools for Korean Text) (0) | 2023.01.25 |
| [개념] 어간 추출(Stemming) 및 표제어 추출(Lemmatization) (0) | 2023.01.22 |
| [개념] 토큰화(Tokenization) (0) | 2023.01.20 |
